问题
单项选择题
函数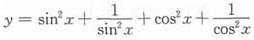 的值域是()。
的值域是()。
A.[5,+∞)
B.(5,+∞)
C.[2,5]
D.(2,+∞)
答案
参考答案:A
解析:
解法1:

=sin2x+csc2x+cos2x+sec2x
=1+1+cot2x+1+tan2x
=3+cot2x+tan2x
因为tan2x+cot2x≥2|tanx|·|cotx|=2,
故当|tanx|=|cotx|,即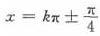 (k∈Z)时,tan2x+cot2x取最小值2,即cot2x+tan2x≥2,
(k∈Z)时,tan2x+cot2x取最小值2,即cot2x+tan2x≥2,
故所求函数y∈[5,+∞),故正确答案为A。
解法2:
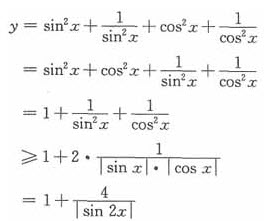
当|sin2x|=1, (k∈Z),即
(k∈Z),即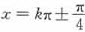 时,|sin2x|取最大值,这时正好有
时,|sin2x|取最大值,这时正好有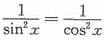 ,则有
,则有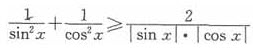 的等号成立,故这时y取最小值1+4=5,故所求函数y∈[5,+∞),故正确答案为A。
的等号成立,故这时y取最小值1+4=5,故所求函数y∈[5,+∞),故正确答案为A。
解法3:

当sin22x=1,

故所求函数y∈[5,+∞),
故正确答案为A。
