问题
解答题
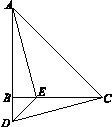
如图,在△ABC中,AB=CB,∠ABC=90º,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
(1) 求证:△ABE≌△CBD;
(2) 若∠CAE=30º,求∠BCD的度数.
答案
证明:如图1.
∵ ∠ABC=90º,D为AB延长线上一点,
∴ ∠ABE=∠CBD=90º .
在△ABE和△CBD中,

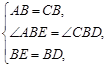
∴ △ABE≌△CBD.
(2)解:∵ AB=CB,∠ABC=90º,
∴ ∠CAB="45°."
又∵ ∠CAE=30º,
∴ ∠BAE =15°.
∵ △ABE≌△CBD,
∴ ∠BCD="∠BAE" =15°.
(1)运用SAS判定三角形全等;
(2)等腰三角形两个底角相等,得出∠CAB=45°,又有△ABE≌△CBD,得到∠BCD=∠BAE。
