问题
问答题
求一个正交变换,化二次型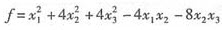 为标准型。
为标准型。
答案
参考答案:
二次型的矩阵是 ,
,
其特征多项式为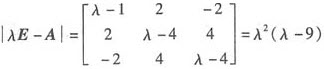 ,
,
所以A的特征值是λ1=λ2=0,λ3=9.
对于是λ1=λ2=0,由(0E-A)x=0,即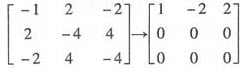
得到基础解系α1=(2,1,0)T,α2=(-2,0,1)T,即为属于特征值λ=0的特征向量.
对于λ3=9,由(9E-A)x=0,即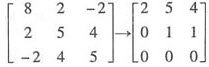 ,
,
得到基础解系α3=(1,-2,2)T.
由于不同特征值的特征向量已经正交,只需对α1,α2正交化.
β1=α1=(2,1,0)T,
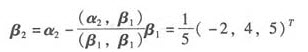
把β1,β2,α3单位化,有

解析:
[考点] 化二次型为标准型的计算
