问题
单项选择题
设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,直线l的斜率取值范围为()。
A.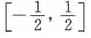
B.[-2,2]
C.[-1,1]
D.[-4,4]
答案
参考答案:C
解析:
因为抛物线的准线为x=-2,
故Q点坐标为(-2,0)。
设过Q点不垂直于x轴的直线方程为y=k(x+2),
代入y2=8x,
化简得k2x2+(4k2-8)x+4k2=0,
若使直线l与抛物线有公共点,则Δ≥0,
故(4k2-8)2-4k2×4k2≥0,
解得-1≤k≤1,
故正确答案为C。
