问题
问答题
设3阶实对称矩阵A的各行元素之和都是3,向量α1=(-1,2,-1)T,α2=(0,-1,1)T是齐次线性方程组AX=0的解.
求正交矩阵Q和对角矩阵Λ使QTAQ=A;
答案
参考答案:令
 ,
,
 . 再将β1,β2单位化:
. 再将β1,β2单位化:

令
 ,则
,则
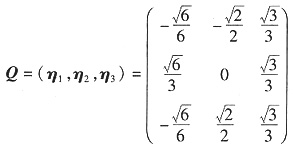
为正交矩阵,使

设3阶实对称矩阵A的各行元素之和都是3,向量α1=(-1,2,-1)T,α2=(0,-1,1)T是齐次线性方程组AX=0的解.
求正交矩阵Q和对角矩阵Λ使QTAQ=A;
参考答案:令
 ,
,
 . 再将β1,β2单位化:
. 再将β1,β2单位化:

令
 ,则
,则
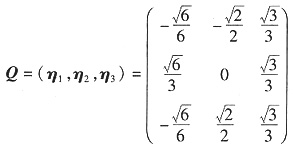
为正交矩阵,使
