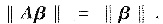设n维列向量，矩阵A=E-4ααT，其中E是n阶单位矩阵，若n维列向量

问题单项选择题

设n维列向量

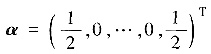，矩阵A=E-4αα^T，其中E是n阶单位矩阵，若n维列向量β=(1，1，…，1)^T，则向量Aβ的长度为

A．

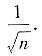
B．

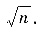
C．n.
D．n².

答案

参考答案：B

解析：利用向量内积可计算出向量的长度，由于

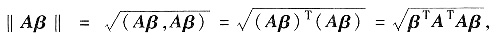
又A^TA=(E-4αα^T)^T(E-4αα^T)=(E-4αα^T)(E-4αα^T)
=E-8αα^T+16α(α^Tα)α^T=E-8αα^T+8αα^T=E，
而

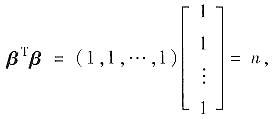
所以

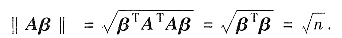故应选B.
注意

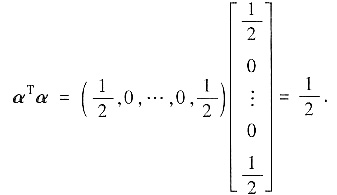
本题考查用内积求向量的长度. 因为本题中所给矩阵A是正交矩阵，因而可看出经正交变换向量的长度不变，即