问题
问答题
已知X1，…，Xn是来自总体X容量为n的简单随机样本，其均值和方差分别为
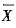与S2．
(Ⅰ) 如果EX=μ，DX=σ2，试证明：
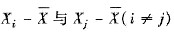的相关系数
；
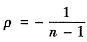(Ⅱ) 如果总体X服从正态分布N(0，σ2)，试证明：协方差cov(X1，S2)=0．
答案
参考答案：[分析与证明] (Ⅰ)由于总体分布未知，因此只好应用定义与性质证明．因为X1，…，Xn相互独立且与总体x同分布，故[*]，
[*]
所以
[*]
(Ⅱ) 由于总体X～N(0，σ2)，故EXi=0，DXi=σ2．又
[*]
所以
[*]
其中
[*]
又
[*]
所以
[*]
[*]
故 cov(X1，S2)=0．