问题
问答题
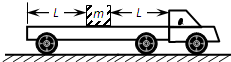
一木箱放在平板车的中部,距平板车的后端、驾驶室后端均为L=1.5m,如图所示处于静止状态,木箱与平板车之间的动摩擦因数为μ=0.5,现使汽车以a1=6m/s2的加速度匀加速启动,速度达到v=6m/s后接着做匀速直线运动,运动一段时间后匀加速刹车求:
(1)当木箱与平板车的速度都达到v=6m/s时,木箱在平板车上的位置;
(2)刹车时为保证木箱不会撞到驾驶室,刹车时时间t'至少应为多少?(g=10m/s2)
答案
(1)设加速运动时木箱的最大加速度为am,
则有 μmg=mam
解得 am=μg=5m/s2
由v=at1得,t1=
=v am
s=1s,即经过t1=1s时车的速度达到6m/s,而此时木箱的速度为v2=amt1=5m/s6 6
木箱还需要加速t2=
=v-v2 a1
s=0.2s才能与车一起匀速运动,这一过程车总共前进 s1=6-5 5
a1 2
+vt2=4.2mt 21
木箱前进 s2=
am(t1+t2)2=3.6m1 2
则木箱相对车后退△s=s1-s2=0.6m.故木箱离车后端0.9m.
(2)刹车时木箱离驾驶室s=2.1m,设木箱至少要前进s3距离才能停下,则
s3=
=3.6m0-v2 2a1
汽车刹车时间为t′,则s3-
t′=s0+v 2
解得,t′=0.5s
答:
(1)当木箱与平板车的速度都达到v=6m/s时,木箱在平板车上离后端0.9m处;
(2)刹车时为保证木箱不会撞到驾驶室,刹车时时间t'至少应为0.5s.
