袋子中装有2个红球,1个黄球,它们除颜色外其余都相同．小明和小英

问题解答题

袋子中装有2个红球,1个黄球,它们除颜色外其余都相同．小明和小英做摸球游戏,约定游戏规则是：小英先从袋中任意摸出1个球记下颜色后放回,小明再从袋中摸出1个球记下颜色后放回,如果两人摸到的球的颜色相同则小英赢,否则小明赢．

（1）请用树状图或列表格法表示一次游戏中所有可能出现的结果;

（2）这个游戏规则公平吗？请说明理由.

答案

（1）表格见解析;（2）这个游戏对双方不公平．

题目分析：（1）2次实验,每次实验都有3种情况,列举出所有情况即可;

（2）看两人摸到的球的颜色相同的情况占所有情况的多少即可求得小明赢的概率,进而求得小英赢的概率,比较即可．

试题解析：（1）根据题意,列表格如下：

所以,游戏中所有可能出现的结果有以下9种：红₁红₁,红₁红₂,红₁黄,红₂红₁,

红₂红₂,红₂黄,黄红₁,黄红₂,黄黄,这些结果出现的可能性是相等的;

（2）这个游戏对双方不公平．理由如下：

由（1）可知,一次游戏有9种等可能的结果,其中两人摸到的球颜色相同的结果有5种,两人摸到的球颜色不同的结果有4种．

∴P（小英赢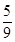）=,P（小明赢）=,

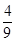∵P（小英赢）≠P（小明赢）,

∴这个游戏对双方不公平．