问题
解答题
为了决定谁将获得仅有的一张科普报告入场券,甲和乙设计了如下的摸球游戏:在不透明口袋中放入编号分别为1、2、3的三个红球及编号为4的一个白球,四个小球除了颜色和编号不同外,其它没有任何区别,摸球之前将袋内的小球搅匀,甲先摸两次,每次摸出一个球(第一次摸后不放回),把甲摸出的两个球放回口袋后,乙再摸,乙只摸一次且摸出一个球,如果甲摸出的两个球都是红色,甲得1分,否则,甲得0分,如果乙摸出的球是白色,乙得1分,否则乙得0分,得分高的获得入场券,如果得分相同,游戏重来.
(1)运用列表或画树状图求甲得1分的概率;
(2)请你用所学的知识说明这个游戏是否公平?
答案
(1)图形见解析,P(甲)=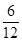 =
=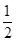 ;
;
(2)不公平.
题目分析:(1)首先根据题意列出表格或画出树状图,然后求得所有等可能的结果与甲得1分的情况,然后利用概率公式求解即可求得答案;
(2)由(1)求得乙的得分,比较概率不相等,即可得这个游戏是不公平.
试题解析:(1)列表得:
| 1 | 2 | 3 | 4 | |
| 1 | ﹣ | 1分 | 1分 | 0分 |
| 2 | 1分 | ﹣ | 1分 | 0分 |
| 3 | 1分 | 1分 | ﹣ | 0分 |
| 4 | 0分 | 0分 | 0分 | ﹣ |

∴P(甲)=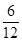 =
=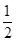
(2)不公平.
∵P(乙)=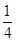
∴P(甲)≠P(乙),
∴不公平.
