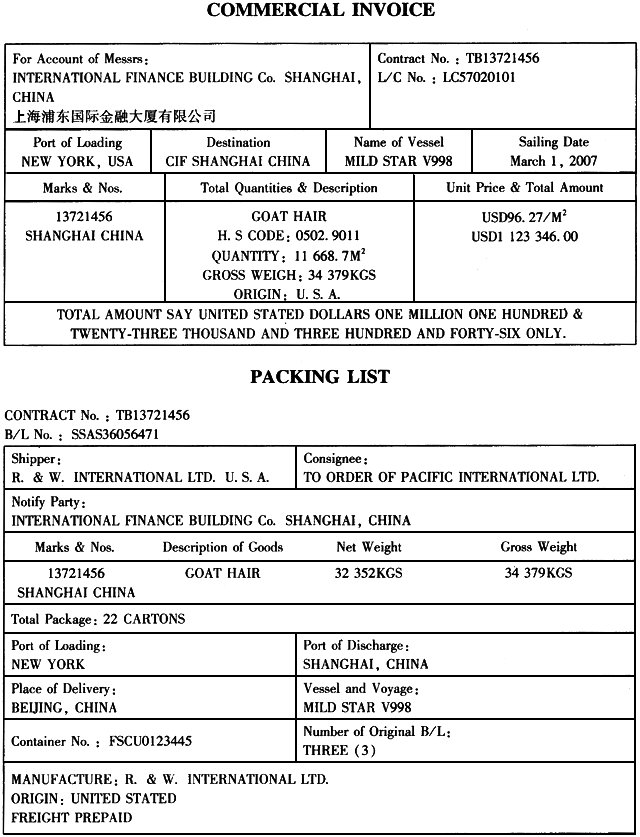
问题
解答题
已知椭圆
|
答案
由e=
,则a2=4b2,椭圆可以转化为:x2+4y2=4b23 2
将y=
x+1代入上式,消去y,得:x2+2x+2-2b2=01 2
直线y=
x+1与椭圆相交有两个不同的点A,B1 2
则△=4-4(2-b2)>0
设A(x1,y1),B(x2,y2),M(x,y)
则
=OM 1 2
+OA 3 2
得OB x=
(x1+1 2
x2)3 y=
(y1+1 2
y2)3
又因为M在椭圆上,所以
+( y1+(x1+
x2)23 4
y2)2 =4b23
代入整理可得,x1x2+4y1y2=0
所以,x1x2+4(1+
x1)(1+1 2
x2)=01 2
x1x2+x1+x2+2=0
因为,x1+x2=-2,x1x2=2-2b2,所以b2=1
所以
+y2=1x2 4