问题
解答题
设a为实数，函数f（x）=x2-2|x-a|-1，x∈R。
（1）若函数f（x）是偶函数，试求实数a的值；
（2）在（1）条件下，写出函数f（x）的单调区间（不要求证明）；
（3）王平同学认为：无论a取任何实数，函数f（x）都不可能为奇函数。你同意他的观点吗？请说明理由。
答案
解：（1）∵函数f（x）是偶函数，∴f（-x）=f（x）在R上恒成立，
即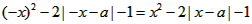
，解得a=0；
（2）由（1）可知a=0，此时函数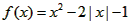
，
∴函数f（x）的单调增区间为（-1，0），（1，+∞）；单调减区间为（-∞，-1），（0，1）
（3）王平的观点是正确的。
若函数f（x）为定义在R上的奇函数，则f（0）=0 但无论a取任何实数，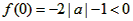
∴函数f（x）都不可能为奇函数。