问题
解答题
二次函数f(x)满足f(x+1)﹣f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若不等式f(x)>2x+m在区间,[﹣1,1]上恒成立,求实数m的取值范围.
答案
解:(1)由f(0)=1,可设f(x)=ax2+bx+1(a≠0)
∵f(x+1)﹣f(x)=2x,
∴a(x+1)2+b(x+1)+1﹣(ax2+bx+1)=2ax+a+b
由题意得,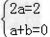 ,解得
,解得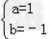 ;
;
故f(x)=x2﹣x+1
(2)由题意得,x2﹣x+1>2x+m 即x2﹣3x+1>m 对x∈[﹣1,1]恒成立,
令g(x)=x2﹣3x+1,
又g(x)在[﹣1,1]上递减,
故g(x)min=g(1)=﹣1故m<﹣1
