问题
选择题
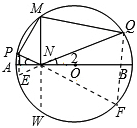
如图,AB是⊙O的直径,M是⊙O上的一点,MN⊥AB,垂足为N,P,Q分别为弧AM、弧BM上一点(不与端点重合)如果∠MNP=∠MNQ,给出下列结论:
①∠1=∠2;②∠P+∠Q=180°;③∠Q=∠PMN;④MN2=PN•QN;⑤PM=QM
其中结论正确的序号是( )
A.①②③
B.①③④
C.①③⑤
D.④⑤
答案
答案:B
解:延长MN交圆于点W,延长QN交于圆点E,延长PN交于圆点F,连接PE,QF
∵∠PNM=∠QNM,MN⊥AB,
∴∠1=∠2(故①正确),
∵∠2与∠ANE是对顶角,
∴∠1=∠ANE,
设圆心为O,连接PO=OE,
∴△APN≌△AEN,
∴PN=EN,
同理NQ=NF,
∵点N是MW的中点,MN•NW=MN2=PN•NF=EN•NQ=PN•QN(故④正确),
∴MN:NQ=PN:MN,
∵∠PNM=∠QNM,
∴△NPM∽△NMQ,
∴∠Q=∠PMN(故③正确).
故选B
