问题
解答题
某工程队要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人的月工资分别为600元和1000元.现要求乙种工种的人数不少于甲种工种人数的2倍.设招聘甲种工种的工人是x人,所聘工人共需付月工资y元.
(1)写出y与x的函数关系式;
(2)甲乙两种工种各招聘多少人时,可使每月所付的工资最少?
答案
设招聘A工种工人x名,则设招聘B工种工人(150-x)名,
依题意得:
,150-x≥2x x≥0
解得:0≤x≤50;
设每月所支付工人工资y元,则y=600x+1000(150-x)=-400x+150000(0≤x≤50);
(2)因为k=-400<0,所以一次函数y随x的增大而减少,
所以当x=50时,y有最少值y=-400x+150000=-400×50+150000=130000(元),
故招聘A工种工人50名,则设招聘B工种工人(150-50)=100(名),
答:招聘A,B工种工人各位50名,100名,支付工人工资130000元的最少值.

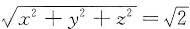 所确定的函数z=z(x,y)在点(1,0,-1)处的全微分dz=______.
所确定的函数z=z(x,y)在点(1,0,-1)处的全微分dz=______.