问题
多项选择题
设f(x)在[a，b]上具有二阶导数，且f"(x)≠0，f(a)=f(b)=0，试证：
(Ⅰ)
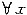∈(a，b)，有f(x)≠0；
(Ⅱ)
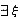∈(a，b)，使f’(ξ)=f(ξ)．
答案
参考答案：若[*]∈(a，b)，使f(x0)=0,f(x)在区间[a，x0]上满足罗尔定理条件，则至少存在一点ξA∈(a，x0)，使f’(ξA)=0．同理，存在一点ξB∈(x0，b)，使f’(ξB)=0．于是f’(x)在区间[ξA，ξB]上满足罗尔定理条件，因此，至少存在一点ξ∈(ξA，ξB)，使f"(ξ)=0．这与题设f"(x)≠0相矛盾，故[*]∈(a，b)，有f(x)≠0．
(Ⅱ)令辅助函数F(x)=e-xf(x)，则
F(a)=e-af(a)=0，F(b)=e-Ff(b)=0,
且由题设知，F(x)在[a，b]上连续，在(a，b)内可导，故由罗尔定理，至少存在一点ξ∈(a，b)，使F’(ξ)=0，即
[*]
因e-ξ≠0，故f’(ξ)=f(ξ)=0，即
f’(ξ)=f(ξ)．
解析：
[分析]： 欲证(Ⅰ)，正面证明不易处理，可采用反证法，结合罗尔定理加以证明．证明(Ⅱ)，先构造辅助函数，再用罗尔定理即可．
