（1）由题意可知：双曲线C的焦点在x轴上，可设此双曲线C的方程为

x2

a2

-

y2

b2

=1（a＞0，b＞0）．

则

b a = 3 3 6 a2 - 1 b2 =1

，解得

a2=3 b2=1

．

∴双曲线C的方程为

x2

3

-y2=1；

（2）设A（x₁，y₁），B（x₂，y₂）．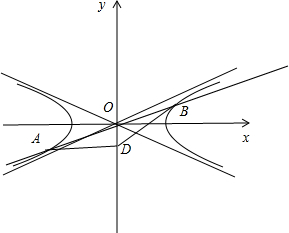

联立

y=kx+m x2-3y2=3

，化为（1-3k²）x²-6kmx-3m²-3=0，（1-3k²≠0）

由题意△＞0，化为m²+1＞3k²．（*）

∴x1+x2=

6km

1-3k2

，x1x2=

-3m2-3

1-3k2

．

设线段AB的中点为M（x₀，y₀），则x0=

x1+x2

2

=

3km

1-3k2

，y₀=kx₀+m=

3k2m

1-3k2

+m=

m

1-3k2

．

∴M(

3km

1-3k2

，

m

1-3k2

).kMD=

m+1-3k2

3km

．

∵|AD|=|BD|，∴k_AB•k_MD=-1．

∴k•

m+1-3k2

3km

=-1，化为4m+1=3k²，代入（*）得m²+1＞4m+1，

解得m＞4或m＜0．

由3k²=4m+1≥0，解得m≥-

1

4

∴m的取值范围是[-

1

4

，0）∪（4，+∞）．