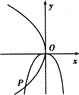
解：(1)因为点P在第三象限，

所以满足条件的抛物线（如图）的标准方程可以是y²=-2p₁x(p₁>0)或x²=-2p₂y(p₂>0)，

解得p₁=4，p₂=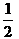    

因此，满足条件的抛物线有两条，它们的标准方程分别为y²= -8x和x²=-y.    

(2)对于直线方程3x-4y-12=0，

令x=0，得y=-3;令y=0，得x=4，    

∴抛物线的焦点为（0，-3）或(4，0).

当焦点为（0，-3）时，，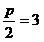

∴p=6，此时抛物线的标准方程为x²=-12y；

当焦点为(4，0)时，，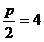

∴p=8，此时抛物线的标准方程为y²=16x，    

∴满足条件的抛物线有两条，它们的标准方程分别为x²=-12y和y²=16x．