问题
问答题
已知函数z=f(x，y)的全微分dz=2xdx-2ydy，并且f(1，1)=2．求f(x，y)在椭圆域
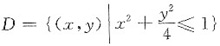上的最大值和最小值．
答案
参考答案：
[分析]： 根据全微分和初始条件可先确定f(x，y)的表达式．而f(x，y)在椭圆域上的最大值和最小值，可能在区域的内部达到，也可能在区域的边界上达到，且在边界上的最值又转化为求条件极值．
[详解] 由题设，知
，
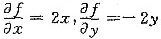于是f(x，y)=x2+C(y)，且C’(y)=-2y，从而C(y)=-y2+C，
再由f(1，1)=2，得C=2，故f(x，y)=x2-y2+2．
令
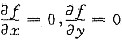得可能极值点为x=0，y=0．且
，
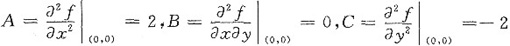△=B2-AC=4＞0，所以点(0，0)不是极值点，从而也非最值点．
再考虑其在边界曲线
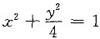上的情形：令拉格朗日函数为
，
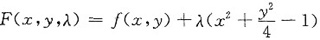解
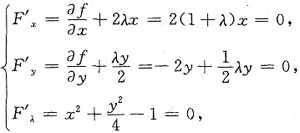
得可能极值点x=0，y=2，λ=4；x=0，y=-2，λ=4；x=1，y=0，λ=-1；x=-1，y=0，λ=-1．代入f(x，y)得f(0，±2)=-2，f(±1，0)=3，
可见z=f(x，y)在区域
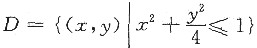内的最大值为3，最小值为-2．
