问题
单项选择题
设A为n阶实矩阵，AT为A的转置矩阵，则对于线性方程组（Ⅰ）Ax=0和（Ⅱ）ATAX=0必有（）.
A．(Ⅱ)的解是(Ⅰ)的解，但(Ⅰ)的解不是(Ⅱ)的解
B．(Ⅱ)的解是(Ⅰ)的解，(Ⅰ)的解也是(Ⅱ)的解
C．(Ⅰ)的解不是(Ⅱ)的解，(Ⅱ)的解也不是(Ⅰ)的解
D．(Ⅰ)的解是(Ⅱ)的解，但(Ⅱ)的解不是(Ⅰ)的解
答案
参考答案：B
解析：
线性方程组的解
若xi是AX=0的解，即Axi=0，显然ATAxi=0；
若xi是ATAX=0的解，即ATAxi=0，则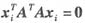
，即(Axi)T(Axi)=0．
若Axi≠0，不妨设Axi=(b1，b2，…，bn)T，b1≠0，则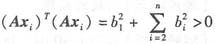
，与(Axi)T(Axi)=0矛盾，因而Axi=0，即(Ⅰ)、(Ⅱ)同解．选(B)．