参考答案：因为任一个n维非零列向量均是A的特征向量，故A有n个线性无关的特征向量，从而A必与对角矩阵相似.
现取n个单位向量
ε_i=(0，…，0，1，0，…，0)^T，(i=1，2，…，n)
为A的特征向量，其特征值分别为λ₁，λ₂，…，λ_n，那么令P=(ε₁，ε₂，…，ε_n)=E，有

即

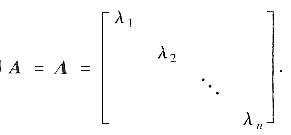
如果λ₁≠λ₂，则A(ε₁+ε₂)=λ₁ε₁+λ₂ε₂.
因为每个n维向量都是A的特征向量，又应有A(ε₁+ε₂)=λ(ε₁+ε₂)，于是
(λ₁-λ)ε₁+(λ₂-λ)ε₂=0.
由于λ₁-λ，λ₂-λ不全为0，与ε₁，ε₂线性无关相矛盾，所以必有λ₁=λ₂.
同理可知λ₁=λ₂=…=λ_n=k，故A=kE.

解析：n阶数量矩阵kE的特征值是k(n重根)，并且任一n维非零列向量都是kE的特征向量。