问题
解答题
等边△ABC的边长为a，求其内切圆的内接正方形DEFG的面积．
答案
等边△ABC的边长为a，
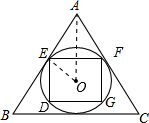
∵点O为△ABC的内心，
∴OE⊥AB，AE=BE=
，∠EAO=30°，a 2
∴OE=AE?tan∠EAO=
a，3 6
则正方形的边长是OE?cos45°=
OE=2 2
a．6 6
则正方形的面积是：
a2．1 6
搜题请搜索小程序“爱下问搜题”
等边△ABC的边长为a，求其内切圆的内接正方形DEFG的面积．
等边△ABC的边长为a，
∵点O为△ABC的内心，
∴OE⊥AB，AE=BE=
，∠EAO=30°，a 2
∴OE=AE?tan∠EAO=
a，3 6
则正方形的边长是OE?cos45°=
OE=2 2
a．6 6
则正方形的面积是：
a2．1 6