问题
问答题
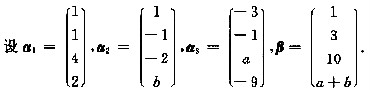
(Ⅰ) 当a,b为何值时,β不可由α1,α2,α3线性表示;
(Ⅱ) 当a,b为何值时,β可由α1,α2,α3线性表示,写出表达式.
答案
参考答案:[*]
1) 当a≠-6,a+2b-4≠0时,因为[*],所以β不可由α1,α2,α3线性表示;
2) 当a≠-6,a+2b-4=0时,[*],β可由α1,α2,α3唯一线性表示,表达式为β=2α1-α2+0α3;
当a=-6时,
[*]
当a=-6,b≠5时,[*],β可由α1,α2,α3唯一线性表示,表达式为β=6α1+lα2+2α3;
当a=-6,b=5时,[*],β可由α1,α2,α3线性表示,表达式为β=(2k+2)α1+(k-1)α2+kα3,其中k为任意常数.
