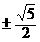问题
解答题
已知直线y=kx-1与双曲线x2-y2=4
(1)若直线与双曲线没有公共点，求k的取值范围；
(2)若直线与双曲线有两个公共点，求k的取值范围；
(3)若直线与双曲线只有一个公共点，求k的取值范围．
答案
解：由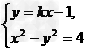
得（1-k2）x2+2kx-5=0.①
(1)直线与双曲线没有公共点，则①式方程无解．
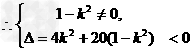解得
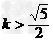或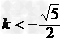
则k的取值范围为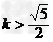
或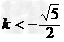
(2)直线与双曲线有两个公共点，
则①式方程有两个不相等的根．
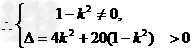解得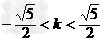
且k≠±1．
(3)直线与双曲线只有一个公共点，则①式方程只有一解．
当1-k2=0，
即k=±1时，①式方程只有一解；
当1-k2≠0时，应满足Δ=4k2+20（1-k2）=0，解得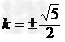
故k的值为±1或