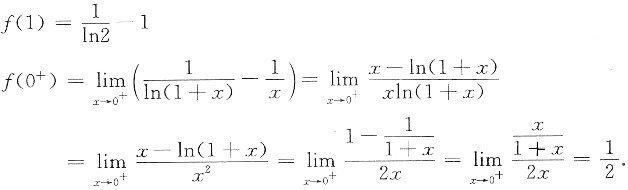问题
问答题
设x∈(0,1),证明:
(1)(1+x)ln2(1+x)<x2; (2)
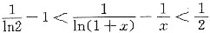 .
.
答案
参考答案:[证明] (1)令φ(x)=x2-(1+x)ln2(1+x),则
φ’(x)=2x-ln2(1+x)-2ln(1+x)
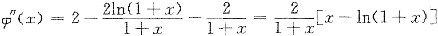
又
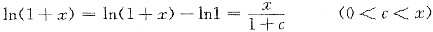
<x x∈(0,1)
则φ"(x)>0 x∈(0,1)
φ’(x)>φ’(0)=0 x∈(0,1)
φ(x)>φ(0)=0 x∈(0,1)
故(1+x)ln2(1+x)<x2
(2)令
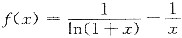
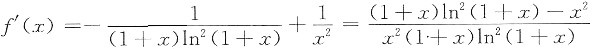
由(1)知f’(x)<0, x∈(0,1)
则f(x)在(0,1)上单调减,
f(1)<f(x)<f(0+) x∈(0,1)