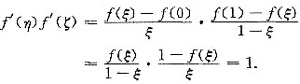问题
问答题
已知函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1.证明:(Ⅰ)存在ξ∈(0,1),使得f(ξ)=1-ξ;
(Ⅱ)存在两个不同的点η,ξ∈(0,1),使得f’(η)f’(ξ)=1.
答案
参考答案:[证明] (Ⅰ)令F(x)=f(x)-1+x x∈[0,1]
由题设知,F(x)在[0,1]上连续,又
F(0)=f(0)-1=-1<0,F(1)=f(1)=1>0
由连续函数的零点定理知,存在ξ∈(0,1),使得F(ξ)=0,
即
f(ξ)=1-ξ.
(Ⅱ)在区间[0,ξ]和[ξ,1]上分别对f(x)用拉格朗日中值定理得
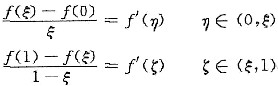
此时,