参考答案：

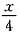sin2x+C₁cos2x+C₂sin2x，其中C₁与C₂是两个任意常数．

解析： y"+4y=cos2x对应的齐次方程的特征方程是r²+4=0．它的两个特征根为r_1,2=±2i．
因此对应的齐次方程的通解为Y=C₁cos2x+C₂sin2x．
又因±ωi=±2i是特征方程的根，所以，应设非齐次方程的特解为
y^*=x(Acos2x+Bsin2x)，
则(y^*)’=x(-2Asin2x+2Bcos2x)+Acos2x+Bsin2x，
(y’)"=-x(4Acos2x+4Bsin2x)-4Asin2x+4Bcos2x．
将上两式代入方程y"+4y=cos2x得
-4Asin2x+4Bcos2x=cos2x．
比较系数得A=0，B=

．
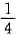这是一个二阶常系数线性非齐次方程的求解问题，容易犯的错误是将非齐次方程的特解设为y^*=xAcos2x，注意，当二阶方程具有y"+4y=pcos2x或y"+4y=qsin2x或y"+4y=pcos2x+qsin2x等形式，且其中p，q是不等于零的常数时，其特解都应设为y^*=x(Acos2x+Bsin2x)．