问题
问答题
已知n维列向量α1,α2,…,αs非零且两两正交,证明α1,α2,…,αs线性无关.
答案
参考答案:证明 (定义法,同乘).若k1α1+k2α2+…+ksαs=0,用[*]左乘上式,得
[*]
由于α1与α2,…,αn均正交,有[*](i=2,…,s).
从而 [*]又因α1≠0知||α1||≠0,得到k1=0.
同理可证k2=0,…,ks=0,因此,向量组α1,α2,…,αs线性无关.
解析:分析 向量α,β正交,即内积为0,即αTβ=βTα=0.
[*]

 m+
m+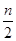 -3p)mol
-3p)mol