参考答案：

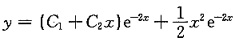，其中C₁，C₂为任意常数

解析：[详解] 特征方程为

，
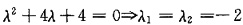所以原方程对应的齐次方程的通解为y=(C₁+C₂x)e^-2x，
由于非其次项为e^-2x，所以可设特解为y^*=Ax²e^-2x，于是有
y^*’=2Axe^-2x-2Ax²e^-2x，y^*"=2Ae^-2x-8Axe^-2x+4Ax²e^-2x，
代入方程y"+4y’+4y=e^-2x可解得

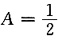，即

，
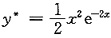所以所求方程的通解为

，
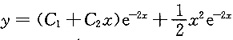其中C₁，C₂为任意常数．