问题
填空题
若函数f(x)=
|
答案
因为f(x)为奇函数,所以f(-1)=-f(1),即1-m=-(-1+2),解得m=2,
经检验,当m=2时,满足f(-x)=-f(x),
所以m=2,
故答案为:2.
若函数f(x)=
|
因为f(x)为奇函数,所以f(-1)=-f(1),即1-m=-(-1+2),解得m=2,
经检验,当m=2时,满足f(-x)=-f(x),
所以m=2,
故答案为:2.
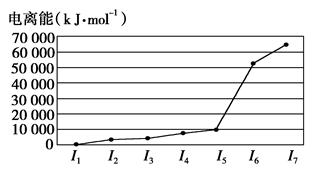
A、B、C、D、E五种元素,A元素的周期数、主族数、原子序数相同;B的基态原子核外有3种能量不同的原子轨道,且每种轨道中的电子数相同;C元素的电离能如图所示;D元素的价电子构型为nsnnpn+2;E是第4周期的过渡元素,血红蛋白中的E元素与BD形成的配位键比与D2形成的配位键强。E单质与BD形成的配合物E(BD)5,常温下呈液态,熔点为-20.5℃,沸点为103 ℃,易溶于非极性溶剂。
C元素的电离能
(1)E(BD)5晶体属于________(填晶体类型)。
(2)A元素和B元素组成的化合物分子之间________(填“能”或“不能”)形成氢键。
(3)基态E原子的电子排布式为___________________________________ 。
(4)B、C、D三种元素的电负性由大到小的顺序是________(填元素符号)。
(5)C2和B2A2的分子中根据电子云重叠的方式不同,都包含的共价键类型有________。
(6)已知原子数和电子数相同的微粒叫等电子体,等电子体的结构相似。根据
下表数据,说明BD分子比C2分子活泼的原因_____________________________。
| X—Y | X=Y | X≡Y | |
| BD的键能/kJ·mol-1 | 357.7 | 798.9 | 1 071.9 |
| C2的键能/kJ·mol-1 | 154.8 | 418.4 | 941.7 |