问题
填空题
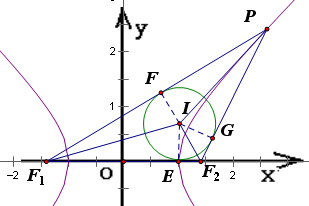
已知点P是双曲线
|
答案
如图,设圆I与△PF1F2的三边F1F2、PF1、PF2分别相切于点E、F、G,连接IE、IF、IG,
则IE⊥F1F2,IF⊥PF1,IG⊥PF2,它们分别是
△IF1F2,△IPF1,△IPF2的高,
∴S△IPF1=
×|PF1|×|IF|=1 2
|PF1|,r 2
S△IPF2=
×|PF2|×|IG|=1 2
|PF2|r 2
S△IF1F2=
×|F1F2|×|IE|=1 2
|F1F2|,其中r是△PF1F2的内切圆的半径.r 2
∵S△IPF1=S△IPF2+
S△IF1F21 2
∴
|PF1|=r 2
|PF2|+r 2
|F1F2|r 4
两边约去
得:|PF1|=|PF2|+r 2
|F1F2|1 2
∴|PF1|-|PF2|=|F1F2|
根据双曲线定义,得|PF1|-|PF2|=2a,|F1F2|=2c
∴2a=c⇒离心率为e=
=2c a
故答案为:2.