问题
填空题
已知f(x)是奇函数,且在(0,+∞)上是减函数,问f(x)的(-∞,0)上的单调性 ______.
答案
由题意可知:任意的x1、x2∈(-∞,0),且x1<x2<0.
∴-x1>-x2>0
因为在(0,+∞)上是减函数,所以f(-x1)<f(-x2)
又因为函数f(x)是奇函数,
∴-f(x1)<-f(x2)
∴f(x1)>f(x2)
∴函数f(x)在(-∞,0)上是减函数.
故答案为:单调减函数.
已知f(x)是奇函数,且在(0,+∞)上是减函数,问f(x)的(-∞,0)上的单调性 ______.
由题意可知:任意的x1、x2∈(-∞,0),且x1<x2<0.
∴-x1>-x2>0
因为在(0,+∞)上是减函数,所以f(-x1)<f(-x2)
又因为函数f(x)是奇函数,
∴-f(x1)<-f(x2)
∴f(x1)>f(x2)
∴函数f(x)在(-∞,0)上是减函数.
故答案为:单调减函数.
读材料一和材料二,完成下列问题。
材料一:河流①中下游河段规划建设十三级水电站,总装机容量达2 132万千瓦,年发电量1 029.6亿千瓦时。该河流是我国仅剩的两条未开发的大河之一。但有专家呼吁:不要在该河流上建坝,保留一条自然的河。
材料二:2006年5月20日,三峡大坝主体工程全面竣工。在过去的10年中,美国建坝的数量大幅度下降,而拆坝的数量在逐年增加,到目前为止,美国已撤除了500多座水坝。下表是近年部分被拆除的水坝。
| 水坝名称 | 建造时间 | 拆除年份 | 作用影响 | |
| 南巴塔维亚水坝 | 20世纪初 | 2003 | 将有利于鱼类迁徙 | |
| 威恩彻斯特水坝 | 不详 | 2002 | 开辟了南美鲱鱼、河鲱鱼、美洲鳗及大西洋鲑的产卵地以及濒危物种矮楔贝的繁殖 | |
| 瓦贝卡水坝 | 19世纪50年代 | 2001 | 恢复了迁徙鲑鱼和鳟鱼的产卵和小吻鲈的栖息地,水质提高,保存印第安人文化,增加公共休闲地 |
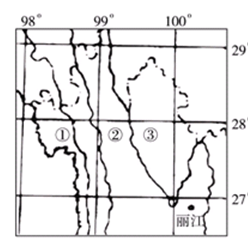
(1)读上图,①是 ,②是 ,③是 。河流②最后注入 洋。
(2)分析河流①水能丰富但至今尚未开发的原因。
(3)专家呼吁,不要在河流①上建坝,保留一条自然的河的理由有哪些?