问题
解答题
已知定义域为R的函数f(x)=
(1)判断其奇偶性并证明; (2)判断函数f(x)在R上的单调性,不用证明; (3)是否存在实数k,对于任意t∈[1,2],不等式f(t2-2t)+f(2t2-k)>0恒成立.若存在,求出实数k的取值范围;若不存在,说明理由. |
答案
(1)f(x)是奇函数.
证明:∵f(-x)=
-1 2-x+1
=1 2
-2x 2x+1
=1-1 2
-1 2x+1
=1 2
-1 2
=-(1 2x+1
-1 2x+1
)=-f(x)1 2
∴f(x)是R上的奇函数.(3分)
(2)由(1)可知f(x)是奇函数,
当x=0时,f(x)=0,
当x>0且x越来越大,f(x)越来越小,x→+∞,f(x)越来越来→-
,1 2
∴f(x)是R上的减函数.(6分)
(3)∵f(x)是R上的奇函数,
∴f(t2-2t)>-f(2t2-k)=f(k-2t2)(9分)
又f(x)是R上的减函数
∴t2-2t<k-2t2
即问题等价于对任意t∈[1,2],k>3t2-2t恒成立(12分)
令g(t)=3t2-2t,
则g(t)在[1,2]上是增函数,
∴g(t)max=g(2)=12-4=8(13分)
∴k>8.

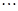 k级台阶,每级台阶的长为30cm,高为15cm(g=10m/s2).某同学从第0级台阶的边缘以v0=5m/s水平抛出一小球(不计一切阻力),则小球将落在第几级台阶上
k级台阶,每级台阶的长为30cm,高为15cm(g=10m/s2).某同学从第0级台阶的边缘以v0=5m/s水平抛出一小球(不计一切阻力),则小球将落在第几级台阶上