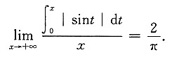问题
问答题
证明
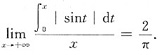
答案
参考答案:[证明]因|sinx|是以π为周期的周期函数,且
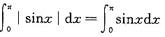 =2,从而当n=1,2,3,…时
=2,从而当n=1,2,3,…时
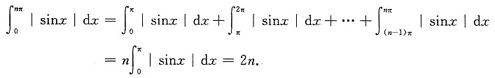
又因当nπ≤x≤(n+1)π时
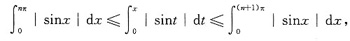
于是有
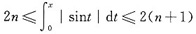 当nπ≤x≤(n+1)π时成立,由不等式的性质即知此时成立
当nπ≤x≤(n+1)π时成立,由不等式的性质即知此时成立
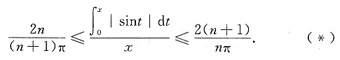
当z→+∞时满足(n+1)π≥x≥nπ的n满足
 ,于是相应的n也满足n→+∞.所以在(*)中令x→+∞取极限,即得
,于是相应的n也满足n→+∞.所以在(*)中令x→+∞取极限,即得
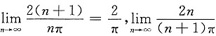
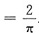 .由夹逼定理即知
.由夹逼定理即知
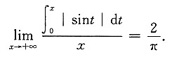
证明
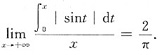
参考答案:[证明]因|sinx|是以π为周期的周期函数,且
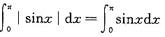 =2,从而当n=1,2,3,…时
=2,从而当n=1,2,3,…时
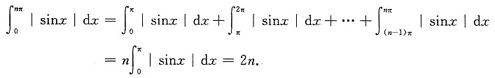
又因当nπ≤x≤(n+1)π时
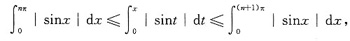
于是有
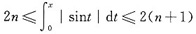 当nπ≤x≤(n+1)π时成立,由不等式的性质即知此时成立
当nπ≤x≤(n+1)π时成立,由不等式的性质即知此时成立
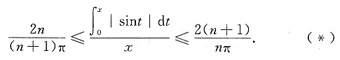
当z→+∞时满足(n+1)π≥x≥nπ的n满足
 ,于是相应的n也满足n→+∞.所以在(*)中令x→+∞取极限,即得
,于是相应的n也满足n→+∞.所以在(*)中令x→+∞取极限,即得
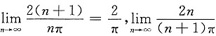
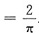 .由夹逼定理即知
.由夹逼定理即知