问题
解答题
为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买x个文具盒,10件奖品共需w元,求w与x的函数关系式。如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
答案
(1) 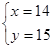 ;(2) 147元.
;(2) 147元.
题目分析:设每个文具盒x元、每支钢笔y元,然后根据花费100元与57元分别列出方程组成方程组,解二元一次方程组即可;根据题设若购买x个文具盒,奖品共有10件,根据以上求得文具盒和钢笔的单价,根据总价等于单价乘以数量得到一个总价与x之间的函数解析式,然后根据函数的性质即可求出最值.
试题解析:(1)设每个文具盒x元,每支钢笔y元,由题意得:
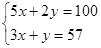 ,解之得:
,解之得: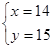 .
.
(2)由题意得:w="14x+15(10-x)=150-x" ,
因为w随x增大而减小, ,∴当x=3时,
,∴当x=3时,
W最大值=150-3=147,即最多花147元.
