问题
问答题
设
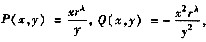其中
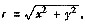
(Ⅰ)选取参数λ，使得
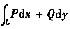在区域D=(x，y)|y＞0内与路径无关；
(Ⅱ)选取参数λ，使得pdx+Qdy在D上存在原函数并求出全体原函数．
答案
参考答案：[分析与求解] (Ⅰ)这里区域D是单连通的，P，Q在D上有连续的偏导数，于是
[*]
即在区域D上
[*]
因此，仅当λ=-1时[*]在D内与路径无关．
(Ⅱ)只要P，Q在D上连续，则
Pdx+Qdy在D上存在原函数[*]在D内与路径无关．
因此，由题(Ⅰ)知，仅当λ=-1时Pdx+Qdy在D存在原函数．下求原函数u(du=Pdx+Qdy)：
方法1° 不定积分法．由[*]
[*]
注意[*]
再由[*]
[*]
因此求得Pdx+Qdy的全体原函数为[*]
方法2° 特殊路径积分法．
[*]
取(x0，y0)=(0，1)及积分路径为折线如右图，则
[*]
[*]
因此，全体原函数为[*]
[*]
