问题
问答题
某市为了进一步改善居民的生活环境,园林处决定增加公园A和公园B的绿化面积,已知公园A、B分别有如图1、图2所示的阴影部分需铺设草坪,在甲、乙两地分别有同种草皮1608m2和1200m2出售,且售价一样.若园林处向甲、乙两地购买草皮,其路程和运费单价见下表:
| 公园A | 公园B | ||
| 路程(千米) | 运算单价(元) | 路程(千米) | 运费单价(元) | |
| 甲地 | 30 | 0.25 | 32 | 0.25 |
| 乙地 | 22 | 0.3 | 30 | 0.3 |
(注:运费单价指将每平方米草皮运送1千米所需的人民币)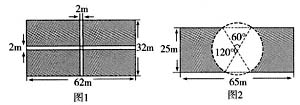
请设计出总运费最省的草皮运送方案,并说明理由。
答案
参考答案:
设总运费为y元,公园A向甲地购买草皮xm2,向乙地购买草皮(1800-x)m2。
由于公园A、B需要购买的草皮面积总数为1800+1008=2808(m2),
甲、乙两地出售的草皮面积总数为1608+1200=2808(m2),
所以,公园B向甲地购买草皮(1608-x)m2,
向乙地购买草皮1200-(1800-x)=(x-600)(m2)。
于是,有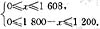
所以600≤x≤1608,又由题意得
y=30×0.25x+22×0.3×(1800-x)+32×0.25×(1608-x)+30×0.3×(x-600)=1.9x+19344
因为函数y=1.9x+19344随x的增大而增大,
所以,当x=600时,有最小值y=1.9×600+19.344=20484(元)。
因此,公园A在甲地购买600m2,在乙地购买1800-600=1200(m2);
公园B在甲地购买1608-600=1008(m2)时,运送草皮的总运费最省。
