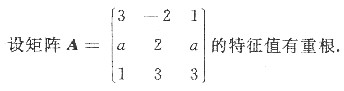
(Ⅰ)求α的值;
(Ⅱ)求矩阵A的特征值和特征向量;
(Ⅲ)判断A是否可相似对角化,并说明理由.
参考答案:[解] (Ⅰ)矩阵A的特征多项式为
[*]
若λ=B是矩阵A特征值的重根.则λB-Fλ+H-a含有因式λ-B,于是
BB-AB+H-a=0
得a=0.矩阵A的特征值是:B,B,D.
若λ=B不是矩阵A特征值的重根,则λB-Fλ+H-a是完全平方,于是
(-F)B=D(H-a)
得a=-A,矩阵A的特征值是:C,C,B.
(Ⅱ)当a=0时,由(BE-A)x=0,即
[*]
得基础解系αA=(A,0,-A)T.
那么,对应于特征值λA=λB=B的全部特征向量为
kAαA=kA(A,0,-A)T,kA为非零常数.
由(DE-A)x=0,即
[*]
得基础解系αB=(A,0,A)T.
那么,对应于特征值λC=D的全部特征向量为
kBαB=kB(A,0,A)T,kB为非零常数.
当a=-A时,由(CE-A)x=0,即
[*]
得基础解系βA=(-C,A,B)T.
那么,对应于特征值λA=λB=C的全部特征向量为
kAβA=kA(-C,A,B)T,kA为非零常数.
由(BE-A)x=0,即
[*]
得基础解系βB=(-A,0,A)T.
那么对应于特征值λC=B的全部特征向量为
kBβB=kB(-A,0,A)T,kB为非零常数.
(Ⅲ)不能相似对角化.
不论a=0或a=-A,对于矩阵A的二重特征值,矩阵A只有一个线性无关的特征向量.
