问题
选择题
已知F1、F2为双曲线C：x2﹣y2=1的左、右焦点，点P在C上，∠F1PF2=60°，则|PF1|•|PF2|=（ ）
A．2
B．4
C．6
D．8
答案
答案：B
法1．由余弦定理得
cos∠F1PF2=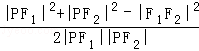
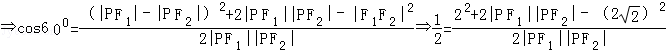
∴|PF1|•|PF2|=4
法2； 由焦点三角形面积公式得：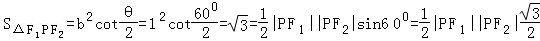
∴|PF1|•|PF2|=4；
故选B．
搜题请搜索小程序“爱下问搜题”
已知F1、F2为双曲线C：x2﹣y2=1的左、右焦点，点P在C上，∠F1PF2=60°，则|PF1|•|PF2|=（ ）
A．2
B．4
C．6
D．8
答案：B
法1．由余弦定理得
cos∠F1PF2=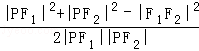
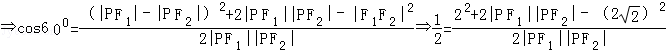
∴|PF1|•|PF2|=4
法2； 由焦点三角形面积公式得：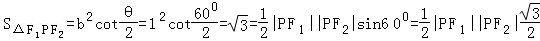
∴|PF1|•|PF2|=4；
故选B．