问题
填空题
圆的一条弦把圆分为度数比为1:5的两条弧,如果圆的半径为4,则弦长为______,该弦的弦心距为______
圆的一条弦长等于它的半径,那么这条弦所对的圆周角的度数为______.
答案
(1)如图,连OA,OB,OC⊥AB于C点

弦AB把⊙O分成1:5的两条弧,弧AB的度数=
×360°=60°,1 6
∴△OAB为等边三角形,
∴AB=OA=4,OC=
AB=23 2
,3
即弦AB=4,弦心距OC=2
.3
(2)如图
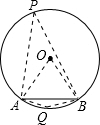
AB为⊙O的弦,且OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠P=
AOB=30°,1 2
∴∠Q=180°-∠P=150°.
即弦AB所对的圆周角为30°或150°.
故答案为4,2
;30°或150°.3
