设函数f(x)和g(x)均有二阶连续导数，满足f(0)＞0，g(0)＜0，并且f’(

问题单项选择题

设函数f(x)和g(x)均有二阶连续导数，满足f(0)＞0，g(0)＜0，并且f^’(0)=g^’(0)=0，那么函数z=f(x)g(y)在点(0，0)处取得极小值的一个充分条件是______

A．f^"(0)＜0，g^"(0)＞0．
B．f^"(0)＜0，g^"(0)＜0．
C．f^"(0)＞0，g^"(0)＞0．
D．f^"(0)＞0，g^"(0)＜0．

答案

参考答案：A

解析：将函数z分别对x和Y求偏导

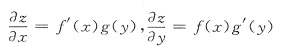
所以有

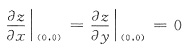
故(0，0)是z的驻点，又

，

，
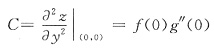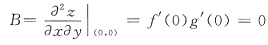于是有 AC-B²=f^"(0)g^"(0)f(0)g(0)．
当f(0)＞0，g(0)＜0，f^"(0)＜0，g^"(0)＞0时A＞0，AC-B²＞0，故x函数取得极小值，所以正确答案为A．