问题
填空题
已知F1、F2是椭圆的两个焦点,满足
|
答案
设椭圆的方程为
+x2 a2
=1(a>b>0),可得F1(-c,0),F2(c,0)y2 b2 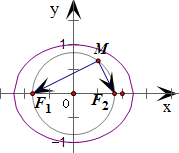
∵
•MF1
=0,MF2
∴M点的轨迹是以原点O为圆心,半焦距c为半径的圆.
又∵M点总在椭圆内部,
∴该圆内含于椭圆,可得c<b,
平方得c2<b2,即c2<a2-c2.
∴e2=
<c2 a2
,可得离心率e满足:0<e<1 2
.2 2
故答案为:(O,
)2 2
