问题
解答题
函数y=lg(3-4x+x2)的定义域为M,当x∈M时,求f(x)=2x+2-3×4x的最值。
答案
解:由3-4x+x2>0,得x>3或x<1,
∴M={x|x>3或x<1},
f(x)=-3×(2x)2+2x+2=-3(2x-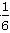 )2+
)2+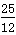
∵x>3或x<1,
∴2x>8或0<2x<2,
∴当2x= ,即x=log2
,即x=log2 时,f(x)最大,最大值为
时,f(x)最大,最大值为 ,
,
f(x)没有最小值。
函数y=lg(3-4x+x2)的定义域为M,当x∈M时,求f(x)=2x+2-3×4x的最值。
解:由3-4x+x2>0,得x>3或x<1,
∴M={x|x>3或x<1},
f(x)=-3×(2x)2+2x+2=-3(2x-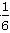 )2+
)2+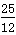
∵x>3或x<1,
∴2x>8或0<2x<2,
∴当2x= ,即x=log2
,即x=log2 时,f(x)最大,最大值为
时,f(x)最大,最大值为 ,
,
f(x)没有最小值。