问题
解答题
在△ABC中，已知（a2+b2）sin（A-B）=（a2-b2）sin（A+B），试判断△ABC的形状。
答案
解：a2sin（A-B）+b2sin（A-B）=a2sin（A+B）-b2sin（A+B）
a2 [sin（A+B）-sin（A-B）]=b2[sin（A-B）+sin（A+B） ]
a2cosAsinB=b2sinAcosB
由题意知 sinB≠0，sinA≠0
则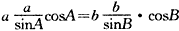
所以acosA=bcosB，由余弦定理，得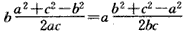
即（a2-b2） （a2+b2-c2）=0
所以a=b或a2+b2=c2
故△ABC为等腰三角形或直角三角形。