问题
解答题
已知集合A={a，b，c}，其中a，b，c是三个连续的自然数．如果a，b，c能够作为一个三角形的三边长，且该三角形的最大角是最小角的2倍，求所有满足条件的集合A．
答案
解：依题意，不妨设a=n﹣1，b=n，c=n+1，
对应的三个内角是α，π﹣3α，2α
由正弦定理，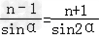
所以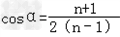
由余弦定理，（n﹣1）2=（n+1）2+n2﹣2（n+1）ncos
即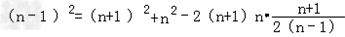
化简，得：n2﹣5n=0
所以，n=0，或n=5，n=0不合题意，舍去．n=5，三角形的三边长为4，5，6．
可以验证此三角形的最大角是最小角的2倍．
故：A={4，5，6}
