若f(n)为n2+1的各位数字之和(n∈N*).如:因为142+1=197,1+9+7=17,所以f(14)=17.记f1(n)=f(n),f2(n)=f(f1(n)),…,fk+1(n)=f(fk(n)),k∈N*,则f2005(8)=______.
因为82+1=65,f1(8)=f(8)=6+5=11,
因为112+1=122,f2(8)=1+2+2=5
因为52+1=26,f3(8)=2+6=8,
所以fk(n)是以3为周期的周期函数.
又2005=3×668+1,∴f2005(8)=f1(8)=11
故答案为:11.

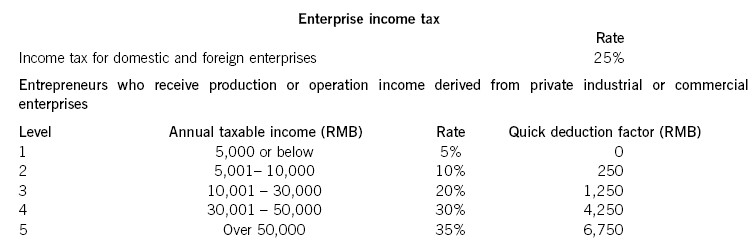


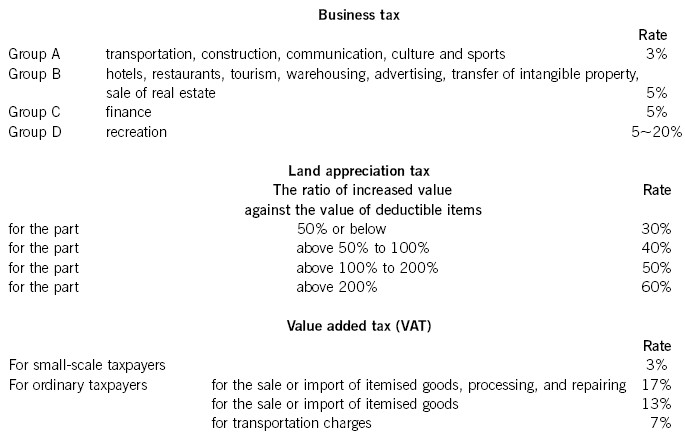

 Required:(i) Briefly explain the tax treatment of losses, including the period for the offset of losses; (2 marks)(ii) State, giving reasons, how much enterprise income tax (EIT) will be payable by Company B for each of the years 2008 and 2009. (4 marks)
Required:(i) Briefly explain the tax treatment of losses, including the period for the offset of losses; (2 marks)(ii) State, giving reasons, how much enterprise income tax (EIT) will be payable by Company B for each of the years 2008 and 2009. (4 marks)