问题
单项选择题
当x→0时，下列无穷小量中阶数最高的是( )．
A．
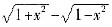
B．3x3-5x5+7x7
C．
-cos x
D．
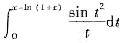
答案
参考答案：D
解析：本题考查无穷小比阶问题，其中第四个选项是复合函数，具有一定的难度．
当x→0时，[*]
3x3-5x5+7x7=x3(3-5x2+7x4)～3x3，
[*]
[*]由[*]与u=x-ln(1+x)复合而成，当x→0时，[*]与x2同阶，[*]，故[*]是x的2×2=4阶无穷小，故选(D)．
[点评] 这里用到一个重要结论：设x→0时，f(x)～xm，g(x)～xn，则
[*]
即f[g(x)]～xmn．