问题
单项选择题
f(x)在[-1,1]连续且函数值只取有理数,则必有 ( )
A.f(x)=x
B.f(x)=xD(x),其中
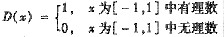
C.f(x)=|x|
D.f(x)=c(c为常数)(x∈[-1,1])
答案
参考答案:D
解析:[考点] 连续函数性质
[答案解析] 应选(D),设不然f(x)≠c(x∈[-1,1]),则存在x1,x2∈[-1,1],设x1<x2,使f(x1)=r1<r2=f(x2),(r1,r2为有理数,r1≠r2,无妨设r1<r2),由无理数的稠密性知,存在无理数a∈(r1,r2)即r1<a<r2,因为已知f(x)在[x1,x2][*][-1,1]上连续,依闭区间上连续函数介值定理,存在ξ∈(x1,x2)[*][0,1],使得有f(ξ)=a.
这与f(x)函数值仅取有理数矛盾,从而f(x)[*]c(x∈[-1,1]),应选(D).
