问题
解答题
在正三角形ABC的边AB、AC上分别取D、E两点，使沿线段DE折叠三角形时，顶点A正好落在边BC上，在这种情况下，若要使AD最小，求AD∶AB的值.
答案
AD∶DB=2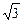
－3
按题意，设折叠后A点落在边BC上改称P点，显然A、P两点关于折线DE对称，又设∠BAP=θ，∴∠DPA=θ，∠BDP=2θ，
再设AB=a，AD=x，∴DP=x
在△ABC中，
∠APB=180°－∠ABP－∠BAP=120°－θ，
由正弦定理知:
∴BP=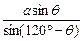
在△PBD中，
,
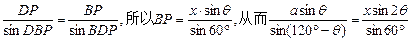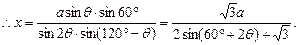
∵0°≤θ≤60°，∴60°≤60°+2θ≤180°，
∴当60°+2θ=90°，即θ=15°时，
sin(60°+2θ)=1，此时x取得最小值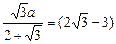
a，即AD最小，
∴AD∶DB=2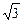－3.
