问题
计算题
解下列方程：
（1）x2﹣2x﹣35=0
（2）3x2+2（x﹣1）=0
（3）7x（5x+2）=6（5x+2）
（4）4（x+1）2=（x﹣3）2．
答案
解：（1）x2﹣2x﹣35=0，
因式分解得：（x﹣7）（x+5）=0，
可化为x﹣7=0或x+5=0，
解得：x1=7，x2=﹣5；
（2）3x2+2（x﹣1）=0，
去括号得：3x2+2x﹣2=0，
∵a=3，b=2，c=﹣2，
∴b2﹣4ac=28＞0，
∴x=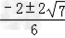
=
，
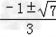∴x1=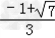
，x2=
；
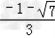（3）7x（5x+2）=6（5x+2），
移项得：7x（5x+2）﹣6（5x+2）=0，
提取公因式得：（5x+2）（7x﹣6）=0，
可化为：5x+2=0或7x﹣6=0，
解得：x1=﹣
，x2=
；
（4）4（x+1）2=（x﹣3）2，
移项得：4（x+1）2﹣（x﹣3）2=0，
因式分解得：[2（x+1）+（x﹣3）][2（x+1）﹣（x﹣3）]=0，
即（3x﹣1）（x+5）=0，
可化为：3x﹣1=0或x+5=0，
∴x1=
，x2=﹣5．